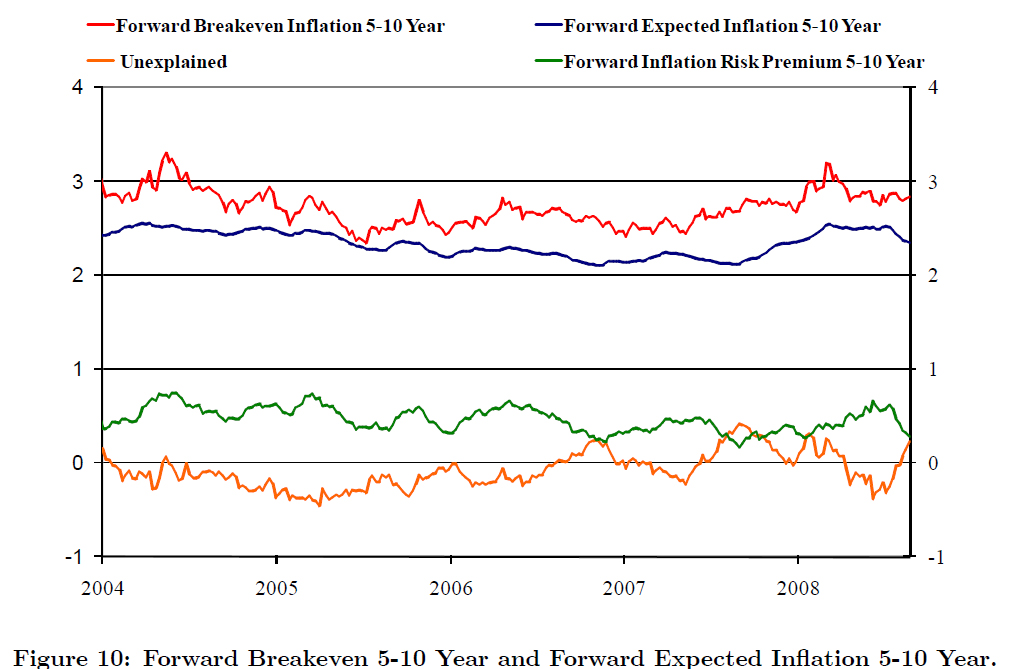
In a working paper published by the Federal Reserve Bank of New York, authored by Tobias Adrian & Hao Wu and titled The Term Structure of Inflation Expectations:
We present estimates of the term structure of inflation expectations, derived from an affine model of real and nominal yield curves. The model features stochastic covariation of inflation with the real pricing kernel, enabling us to extract a time-varying inflation risk premium. We fit the model not only to yields, but also to the yields’ variance-covariance matrix, thus increasing identification power. We find that model-implied inflation expectations can differ substantially from break-even inflation rates when market volatility is high. Our model’s ability to be updated weekly makes it suitable for real-time monetary policy analysis.
They point out:
However, breakeven inflation rates of zero-coupon off-the-run curves (i.e., implied inflation) still are not pure measures of inflation expectations. This is because the absence of arbitrage implies that the difference between zero-coupon nominal and real yields can be decomposed into three components:
Breakeven Inflation = Expected Inflation + Inflation Risk Premium + Convexity
The literature commonly adjust for the convexity effect (see Elsasser and Sack, 2004). However, the adjustment of breakeven inflation for the inflation risk premium requires the estimation of a term structure model.
The paper by Brian P. Sack and Robert Elsasser is titled Treasury Inflation-Indexed Debt: A Review of the U.S. Experience. The convexity complication is explained as:
One complication with interpreting inflation compensation involves the adjustment for convexity. For a given level of the yield on a nominal security, uncertainty about future inflation increases the expected return on that security. This is a mechanical relationship that arises from the convexity of real returns in inflation—specifically, because higher inflation erodes the real return on the security at a slower rate than lower inflation boosts it (see the appendix). This point was originally made by Fischer (1975); a more recent description of the relationship between inflation compensation and future inflation can be found in McCulloch and Kochin (1998).
Although convexity tends to pull down inflation compensation relative to expected inflation, there may be an inflation risk premium that works in the opposite direction.
The methodology of Adrian & Wu is:
In this paper, we develop an affine term structure model that captures the dynamics of real and nominal yields curves, as well as the evolution of their variance-covariance matrix. This is important, as the inflation risk premium is proportional to the conditional covariance of the real pricing kernel and inflation. In order to increase the power for identifying the inflation risk premium, we match both the term structure of the yield curves, and the term structure of variances and covariances.
We find a relatively small and stable inflation risk premium. The order of magnitude of the inflation risk premium is comparable to other recent estimates in studies that use inflation protected bonds over similar sample periods, but it is smaller and less variable than estimates that use nominal bonds and inflation over longer time periods (see Buraschi and Jiltsov, 2005, and Ang, Bekaert, and Wei, 2006).