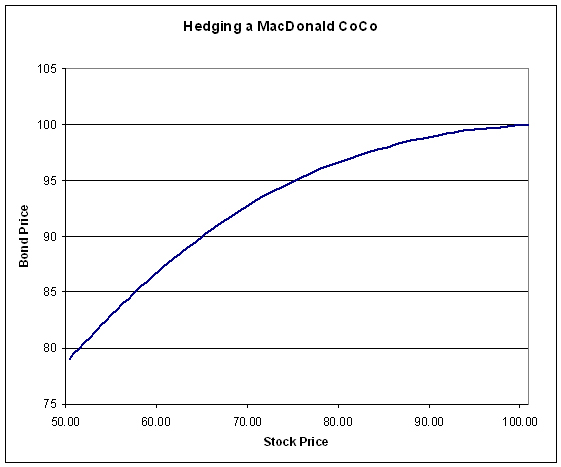
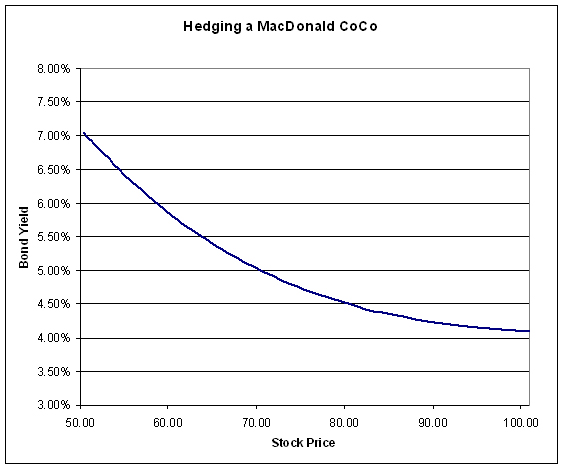
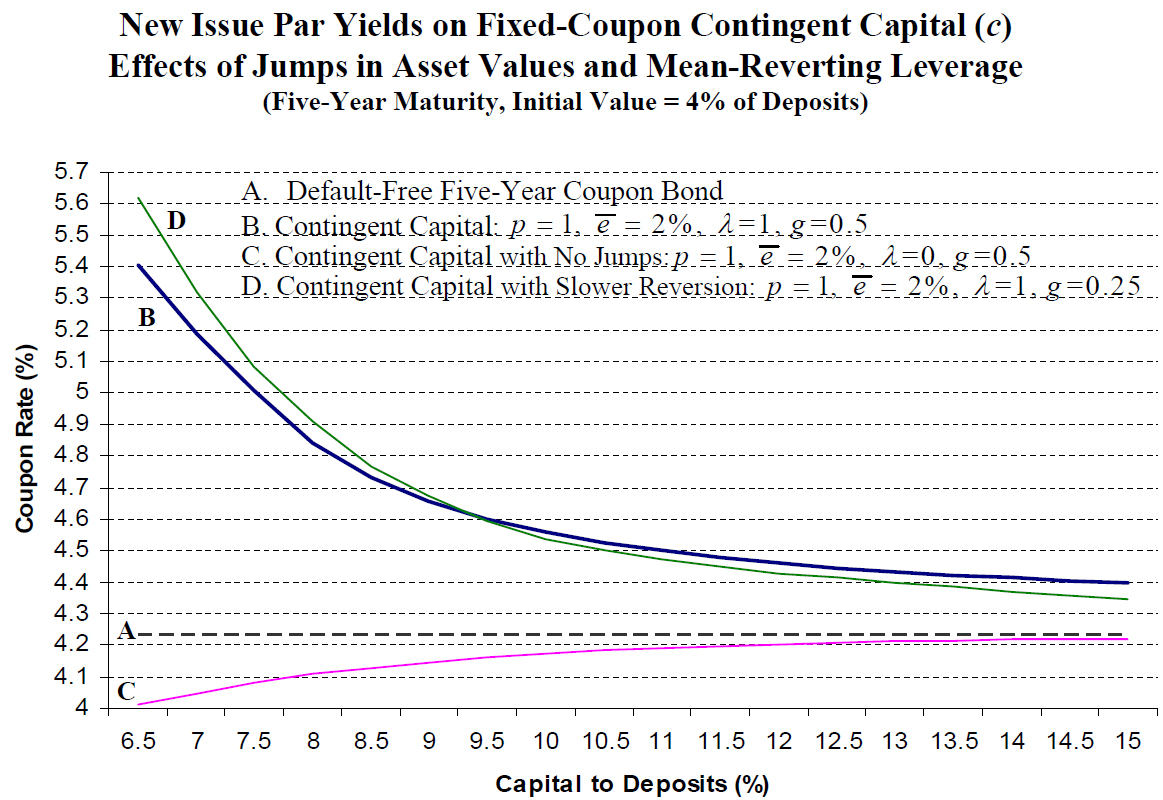
I suspect the propused US financial legislation will have severe and unintended knock-on consequences:
Lawmakers are set to negotiate a bill passed May 20 by the Senate that would require standardized derivative trades to be cleared through a third party and traded on an exchange or so- called swap-execution facility; place a fiduciary duty on dealers in transactions with municipalities; and subject the foreign exchange swaps market to regulation.
…
The bill includes a provision that would require swaps dealers to report price information on a timely basis to the public — a provision designed to increase price transparency. Banks have opposed the language, arguing that it could reduce market liquidity. Gensler has backed the idea, which Stanford’s Duffie called one of “the most important additions” to the debate.“Real time post-trade reporting of transactions is an essential element of a transparent marketplace,” Gensler said last week in his speech. “An effective conference committee report should include these provisions.”
Bond price reporting via TRACE has crippled the US public market in corporate bonds – see, for example, this post – but it doesn’t matter. The legislative climate is such that smooth functioning of the capital markets is not a concern; the concern is transparency, being nice to the little guy and bashing the banks.
The other big problem is fiduciary duty:
The fiduciary duty requirement was crafted in response to swaps deals between Wall Street and local governments designed to keep monthly interest payments low as lending rates change. Such deals often went sour during the economic crisis, pushing one municipality, Jefferson County, Alabama, to the brink of bankruptcy, Lincoln said.
“The bill’s ‘fiduciary duty’ provision would require swap dealers to put the financial interests of state and local governments, retirement plans, pensions and university endowments before its own, ensuring Wall Street doesn’t take advantage of Main Street and taxpayers,” Lincoln said in a June 4 statement provided by her office. “The stories of abuse in this area are alarming and need to be addressed.”
Asset-management firm BlackRock Inc. and some of the largest business trade groups in Washington have argued that imposing a fiduciary duty on deals with municipalities may shut down a market in which, for example, public retirement funds purchase derivatives in order to manage their portfolios.
‘No more buy-side, no more sell-side’ cry the legislators, ‘Capital markets should be a cooperative game, just like the ones we played in kindergarten!’
I suspect that what this will mean in practice is that institutional investors will no longer deal directly with the institutional desk. All orders will have to be routed through a stockbroker (who will probably be completely ignorant), garbled and transmitted. That broker will have to be paid, of course.
What I suspect might happen is that some of the larger asset management firms and hedge funds, not affected by the legislation, will take a more active approach to market-making via dark pools. Being headquartered in Dubai or Singapore will help, of course.
The Financial Crisis Investigation Committe Vice Chairman Bill Thomas demonstrated his integrity and deep committment to justice in the continuing scuffle over Goldman Sachs’ papers:
Blankfein, who has already testified in front of the FCIC along with other bank bosses back in January, is not expected to be asked to testify publicly again. A fired-up Thomas yesterday said the commission has no intention of giving Goldman a chance to make itself look cooperative.
“I’m not interested in providing [Blankfein] with a public forum to sound reasonable when in fact [Goldman’s] behavior has not been.”
Isn’t raking somebody over the coals publicly and under oath supposed to be a good corrective measure for wrongdoing or lack of cooperation? But I guess it’s more fun to vilify someone without giving him a chance to confront his accuser.
Banks’ holdings of each other’s paper – encouraged at the senior debt level by regulators – is attracting attention:
Small lenders, such as Riverside National Bank of Florida, were able to sell trust-preferred securities, known as TruPS, because investment bankers packaged them with those issued by dozens of other financial institutions.
Riverside, which started in a trailer in 1982, bought collateralized debt obligations made up of TruPS as it grew to 65 branches and $4.8 billion assets. When real estate soured and lenders racked up loan losses, Riverside and about 400 of its peers suspended interest payments on their TruPS, causing the CDOs to default or lose value and inflicting more harm on an industry suffering from the worst economy since the 1930s.
…
Congress may end the use of TruPS as capital, forcing banks that issued them to replenish their coffers. Banks are lobbying to remove a provision barring their use that was introduced by Maine Republican Susan Collins and included in the financial reform bill passed by the Senate last month. The Senate version is being reconciled with one passed by the House of Representatives in December that doesn’t include a ban.
It’s a totally asinine reaction. The problem is not that they have issued the TruPS (which are Innovative Tier 1 Capital and, as the story notes, have had their distributions suspended in many cases, which is exactly what’s supposed to happen); the problem is simply that the risk-weighting on the assets is too low. The Fed could change that tomorrow if it felt like it.
If a bank bought $100 of Citigroup shares, it would have to hold $100 of capital against that asset. The purchase of $100 in Citigroup TruPS would require only $8 of capital. For $100 of AAA rated CDOs that pool bank TruPS, the amount of regulatory capital to be set aside declines to $1.60.
And before we start feeling smugly superior to the Americans, up here with our so-called better regulation, remember ING Canada’s 4Q08 balance sheet. However, the provision has been withdrawn:
Banks couldn’t use their TruPS as capital during the financial crisis because deferring the dividends would have been seen as weakness and could have led to bank runs.
“It contributes to a downward spiral,” said George French, the FDIC’s deputy director for policy in the division of supervision and consumer protection.
Trouble continues in Euroland:
Bank credit-default swaps surged near to a record on concern Spanish lenders will have to raise $60 billion to shore up capital as lawmakers struggle to finance a swollen budget deficit.
The Markit iTraxx Financial Index of swaps on 25 European banks and insurers climbed as much as 14 basis points to 208, approaching the all-time closing high of 210 basis points set in March 2009, JPMorgan Chase & Co. prices show. Banco Santander SA, Spain’s biggest bank, increased 23 basis points to a record 258, according to CMA DataVision.
Spanish lenders need as much as 50 billion euros ($60 billion) of capital, according to Banco Bilbao Vizcaya Argentaria SA, as they face mounting writedowns triggered by a housing market collapse and losses on government bond holdings. Civil servants went on strike today to protest at Prime Minister Jose Luis Rodriguez Zapatero’s efforts to tame the euro area’s third-largest deficit.
Another good day in the Canadian preferred share market, with PerpetualDiscounts up 65bp and FixedResets gaining 6bp, on moderate-to-elevated volume.
This is quite a recovery for PerpetualDiscounts! The total return index has returned to its level of March 19; Since March 19, their total return has been -0.35%, compared to -1.73% for FixedResets. Month to date returns have be +2.94% and +0.58%, respectively.
| HIMIPref™ Preferred Indices These values reflect the December 2008 revision of the HIMIPref™ Indices Values are provisional and are finalized monthly |
|||||||
| Index | Mean Current Yield (at bid) |
Median YTW |
Median Average Trading Value |
Median Mod Dur (YTW) |
Issues | Day’s Perf. | Index Value |
| Ratchet | 2.67 % | 2.73 % | 40,665 | 20.66 | 1 | 0.0000 % | 2,093.6 |
| FixedFloater | 5.25 % | 3.34 % | 28,354 | 19.86 | 1 | -1.3810 % | 3,048.1 |
| Floater | 2.41 % | 2.81 % | 89,597 | 20.14 | 3 | -0.2385 % | 2,235.5 |
| OpRet | 4.88 % | 3.78 % | 95,024 | 0.95 | 11 | 0.1026 % | 2,315.7 |
| SplitShare | 6.40 % | -0.29 % | 101,731 | 0.08 | 2 | 0.0442 % | 2,165.3 |
| Interest-Bearing | 0.00 % | 0.00 % | 0 | 0.00 | 0 | 0.1026 % | 2,117.5 |
| Perpetual-Premium | 0.00 % | 0.00 % | 0 | 0.00 | 0 | 0.6540 % | 1,873.2 |
| Perpetual-Discount | 6.05 % | 6.11 % | 203,259 | 13.77 | 77 | 0.6540 % | 1,773.1 |
| FixedReset | 5.45 % | 4.14 % | 408,654 | 3.57 | 45 | 0.0645 % | 2,167.5 |
| Performance Highlights | |||
| Issue | Index | Change | Notes |
| BNS.PR.Y | FixedReset | -1.46 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 24.20 Evaluated at bid price : 24.25 Bid-YTW : 3.77 % |
| BAM.PR.G | FixedFloater | -1.38 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 25.00 Evaluated at bid price : 20.71 Bid-YTW : 3.34 % |
| MFC.PR.B | Perpetual-Discount | 1.01 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 19.05 Evaluated at bid price : 19.05 Bid-YTW : 6.13 % |
| BNS.PR.M | Perpetual-Discount | 1.09 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 19.47 Evaluated at bid price : 19.47 Bid-YTW : 5.87 % |
| CM.PR.E | Perpetual-Discount | 1.12 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 23.22 Evaluated at bid price : 23.51 Bid-YTW : 6.03 % |
| CM.PR.K | FixedReset | 1.15 % | YTW SCENARIO Maturity Type : Call Maturity Date : 2014-08-30 Maturity Price : 25.00 Evaluated at bid price : 26.40 Bid-YTW : 4.07 % |
| PWF.PR.O | Perpetual-Discount | 1.16 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 23.34 Evaluated at bid price : 23.50 Bid-YTW : 6.26 % |
| IAG.PR.E | Perpetual-Discount | 1.16 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 24.15 Evaluated at bid price : 24.35 Bid-YTW : 6.17 % |
| CM.PR.D | Perpetual-Discount | 1.17 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 23.85 Evaluated at bid price : 24.23 Bid-YTW : 6.00 % |
| CM.PR.H | Perpetual-Discount | 1.17 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 19.90 Evaluated at bid price : 19.90 Bid-YTW : 6.12 % |
| TD.PR.R | Perpetual-Discount | 1.18 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 23.80 Evaluated at bid price : 24.00 Bid-YTW : 5.91 % |
| RY.PR.W | Perpetual-Discount | 1.19 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 21.20 Evaluated at bid price : 21.20 Bid-YTW : 5.84 % |
| RY.PR.H | Perpetual-Discount | 1.24 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 24.28 Evaluated at bid price : 24.50 Bid-YTW : 5.81 % |
| RY.PR.B | Perpetual-Discount | 1.28 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 20.53 Evaluated at bid price : 20.53 Bid-YTW : 5.78 % |
| CM.PR.I | Perpetual-Discount | 1.34 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 19.61 Evaluated at bid price : 19.61 Bid-YTW : 6.08 % |
| PWF.PR.K | Perpetual-Discount | 1.40 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 20.32 Evaluated at bid price : 20.32 Bid-YTW : 6.18 % |
| CM.PR.G | Perpetual-Discount | 1.49 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 22.29 Evaluated at bid price : 22.45 Bid-YTW : 6.10 % |
| ELF.PR.F | Perpetual-Discount | 1.55 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 19.60 Evaluated at bid price : 19.60 Bid-YTW : 6.89 % |
| SLF.PR.C | Perpetual-Discount | 1.55 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 18.29 Evaluated at bid price : 18.29 Bid-YTW : 6.10 % |
| PWF.PR.G | Perpetual-Discount | 1.65 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 23.79 Evaluated at bid price : 24.05 Bid-YTW : 6.22 % |
| GWO.PR.I | Perpetual-Discount | 1.66 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 18.41 Evaluated at bid price : 18.41 Bid-YTW : 6.13 % |
| HSB.PR.C | Perpetual-Discount | 1.67 % | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 21.25 Evaluated at bid price : 21.25 Bid-YTW : 6.13 % |
| Volume Highlights | |||
| Issue | Index | Shares Traded |
Notes |
| CM.PR.L | FixedReset | 201,995 | CIBC sold 10,000 to Desjardins at 27.33 and another 10,000 to TD at 27.35. RBC crossed 24,000 at 27.35; CIBC sold another 10,000 to Desjardins at 27.33. Desjardins bought 45,500 from anonymous at 27.38 and crossed 60,000 at 27.36. YTW SCENARIO Maturity Type : Call Maturity Date : 2014-05-30 Maturity Price : 25.00 Evaluated at bid price : 27.35 Bid-YTW : 4.16 % |
| CM.PR.K | FixedReset | 51,640 | RBC crossed 24,000 at 26.45, then 25,000 at 26.35. YTW SCENARIO Maturity Type : Call Maturity Date : 2014-08-30 Maturity Price : 25.00 Evaluated at bid price : 26.40 Bid-YTW : 4.07 % |
| CM.PR.M | FixedReset | 33,760 | YTW SCENARIO Maturity Type : Call Maturity Date : 2014-08-30 Maturity Price : 25.00 Evaluated at bid price : 27.52 Bid-YTW : 4.09 % |
| SLF.PR.G | FixedReset | 27,090 | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 24.51 Evaluated at bid price : 24.56 Bid-YTW : 4.15 % |
| RY.PR.Y | FixedReset | 26,350 | RBC crossed 10,000 at 27.14. YTW SCENARIO Maturity Type : Call Maturity Date : 2014-12-24 Maturity Price : 25.00 Evaluated at bid price : 27.14 Bid-YTW : 4.13 % |
| CM.PR.I | Perpetual-Discount | 24,266 | YTW SCENARIO Maturity Type : Limit Maturity Maturity Date : 2040-06-08 Maturity Price : 19.61 Evaluated at bid price : 19.61 Bid-YTW : 6.08 % |
| There were 33 other index-included issues trading in excess of 10,000 shares. | |||