George Pennacchi, a Professor of Finance at the University of Illinois, has published a paper titled A Structural Model of Contingent Bank Capital that leads to some surprising – to me – conclusions:
This paper develops a structural credit risk model of a bank that issues deposits, share-holders’ equity, and fixed or floating coupon bonds in the form of contingent capital or subordinated debt. The return on the bank’s assets follows a jump-di¤usion process, and default-free interest rates are stochastic. The equilibrium pricing of the bank’s deposits, contingent capital, and shareholders’ equity is studied for various parameter values characterizing the bank’s risk and the contractual terms of its contingent capital. Allowing for the possibility of jumps in the bank’s asset value, as might occur during a financial crisis, has distinctive implications for valuing contingent capital. Credit spreads on contingent capital are higher the lower is the value of shareholders’ equity at which conversion occurs and the larger is the conversion discount from the bond’s par value. The effect of requiring a decline in a financial stock price index for conversion (dual price trigger) is to make contingent capital more similar to non-convertible subordinated debt. The paper also examines the bank’s incentive to increase risk when it issues di¤erent forms of contingent capital as well as subordinated debt. In general, a bank that issues contingent capital has a moral hazard incentive to raise its assetsrisk of jumps, particularly when the value of equity at the conversion threshold is low. However, moral hazard when issuing contingent capital tends to be less than when issuing subordinated debt. Because it reduces e¤ective leverage and the pressure for government bailouts, contingent capital deserves serious consideration as part of a package of reforms that stabilize the financial system and eliminate “Too-Big-to-Fail”.
I am very pleased to see that the structure I have been advocating is receiving academic scrutiny. He discusses the model in terms of the CC proposals of McDonald and Flannery, both of which have been discussed on PrefBlog.
I have difficulty with some of the assumptions:
If a bank’s asset returns follow a pure difusion process without jumps, and fixed-coupon contingent capital converts to shareholders’ equity at its par value, then contingent capital’s new-issue yield-to-maturity (par coupon rate) equals a default-free par rate, such as a Treasury bond yield. But since the possibility of conversion lowers contingent capital’s effective maturity, contingent capital’s comparable default-free yield is less than that of its stated maturity. Thus, if the term structure of default-free Treasury yields is upward sloping, as it normally is, the yield on contingent capital will be less than that of an equivalent-maturity Treasury bond. However, for the case of contingent capital that pays floating-rate coupons, coupon credit spreads above the short-term, default-free interest rate always will be zero.
This assumes that
- The converted noteholder sells his equity immediately upon receipt
- He realizes the trigger price for it (or, as in the case of the McDonald pricing computations discussed elsewhere, very nearly)
This doesn’t work for me. According to me, in order to determine a credit spread, you would have to assume that the converted noteholder hangs on to his equity and sells it on the original maturity date. Assuming immediate sale at the trigger price (nearly) is akin to computing credit spreads due to default with the assumption that the holder can see default coming and sells early.
I suggest that, at the very least, one should look at the discount to market on bank new issues during the crisis (not rights issues, which will often be heavily discounted to ensure take-up; unfortunately this basically eliminates European banks from the sample), and apply this discount to the proceeds on conversion and sale. For example, the CIBC recapitalization was done with the help of a private placement at $62.65 net of fees, compared to its previous close of $72.07. A 14% haircut on conversion – even when converted at par, converting at an explicit discount will be worse – will change the numbers considerably.
Assiduous Readers may make their own assumptions about the effect of the “effective stop-loss order effect” of immediate market orders to sell upon conversion (during a crisis!) according to whatever answers they want to justify. But I don’t think an implicit assumption of 0% frictional or temporal cost is justifiable. It’s too much like assuming 100% recovery on default.
I have more difficulty – similar to my problems with recent advocacy of floating rate contingent capital:
If a bank’s asset returns follow a pure diffusion process without jumps, and fixed-coupon contingent capital converts to shareholders’ equity at its par value, then contingent capital’s new-issue yield-to-maturity (par coupon rate) equals a default-free par rate, such as a Treasury bond yield.
This ignores things like liquidity premia, central bank collateralization premia and default uncertainty, which in this case can be expressed as conversion uncertainty – and that’s just for starters!
I feel compelled to republish one of my favourite graphs, previously shown in the post BoE Releases June 2009 Financial Stability Report:

Arguments that depend on corporate bond yields hugging the green line are doomed to failure, even when the bonds are senior! I will also point out that the liquidity premium on CC is likely to be significantly higher than that on senior bonds, as the investor base is likely to be significantly smaller.
When, more realistically, the bank’s asset returns incorporate a jump process, contingent capital that is speci ed to convert at its par value will have a yield that rises above default-free yields. This positive credit spread is due to the potential losses that contingent capital investors would suffer if a sudden decline in the bank’s asset value requires conversion at below par value. An implication is that new issue credit spreads on contingent capital rise as the bank’s total capital and the value its original shareholders’ equity declines. Credit spreads on contingent capital also are higher the lower is the value of shareholders’ equity at which conversion is specified to occur and the larger is the conversion discount from the bond’s par value. The effect of requiring a decline in a financial stock price index for conversion, the “dual price trigger” feature proposed by McDonald (2009), is to make contingent capital more similar to non-convertible subordinated debt.
The guts of the paper are:
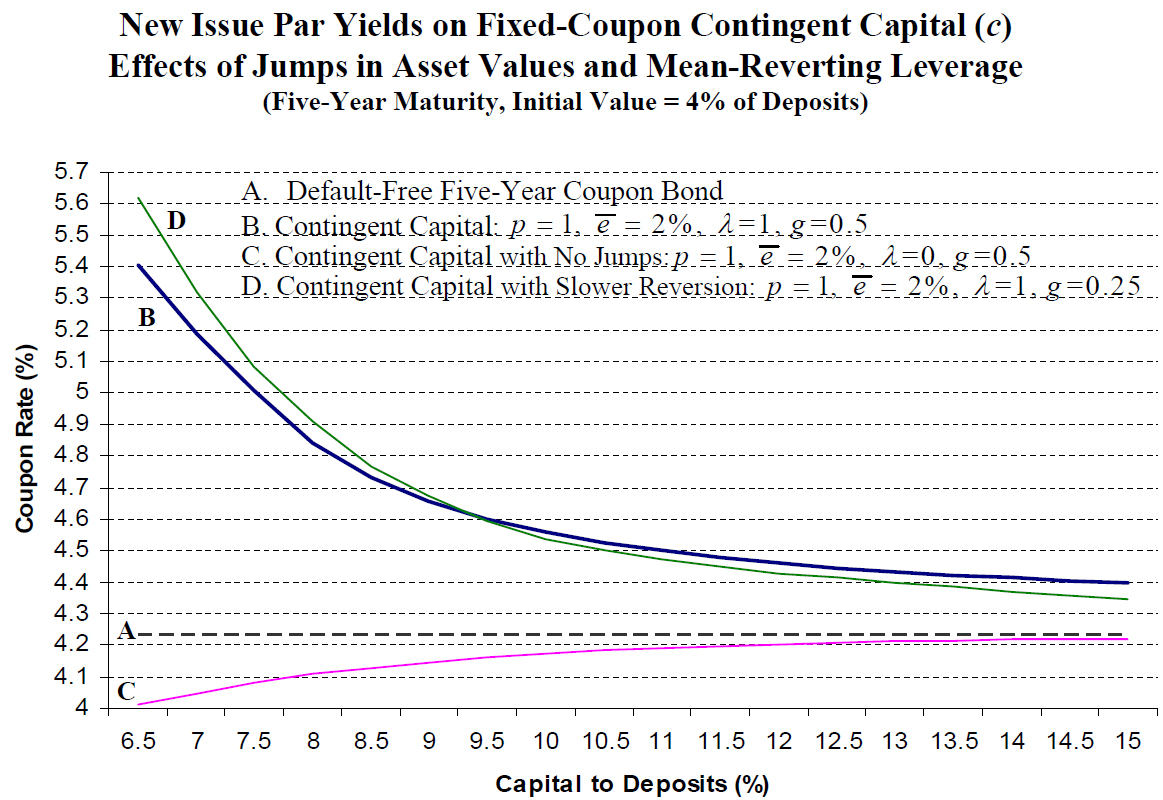
Figure 2 gives the new issue yields for xed-coupon contingent capital, c, when the banks initial total capital ranges from 6.5% to 15%. Recall that the default-free term structure is assumed to have an initial instantaneous maturity interest rate of r0 equal to 3.5% and the par yield on a five-year Treasury coupon bond is 4.23%. This 4.23% default-free, five-year par yield is given by the dashed line denoted Schedule A in the gure. In comparison, Schedule B of Figure 2 shows that the benchmark contingent capital bond’s new issue yield is 5.41%, 4.56%, and 4.39% when initial capital is 6.5%, 10%, and 15%, respectively.
This contingent capital bond’s yield spread above the five-year Treasury is due to the possibility that it could convert at less than par following a downward jump in the bank’s asset (and equity) value. If all of the benchmark parameters are maintained except one assumes there is no possibility of jumps (λ = 0), then the contingent capital bond’s spreads over the five-year Treasury yield would not be positive. Indeed, given the assumption of an upward-sloping term structure, Schedule C of Figure 2 shows that spreads would be slightly negative. Since conversion lowers the e¤ective maturity of contingent capital and, without jumps, it always converts at par, it is e¤ectively a default-free bond with a maturity of less than five years. Hence, its yield is more like a that of a shorter-term default-free bond, which is below the five-year default-free yield. Thus, one sees that the possibility of jumps in the bank’s asset value, as might occur during a financial crisis, has a qualitatively important impact on the pricing of contingent capital.
Other charts include:
- Effect of Maturity
- Effects of conversion terms
- Effects of conversion parameters
- Effect of a Dual Price Trigger
But by me, the most interesting conclusion is:
A bank that issues contingent capital faces a moral hazard incentive to increase its assets’ jump risks. However, this incentive to transfer value from contingent capital investors to the bank’s shareholders is smaller than that when the bank has issued a similar amount of subordinated debt rather than contingent capital. Thus, relative to the status quo, there is likely to be a decline in moral hazard if contingent capital replaces subordinated debt. The results show that excessive risk-taking incentives also decline as contingent capitals equity conversion threshold rises. With a bigger “equity cushion” at the conversion threshold, there is a smaller likelihood that a sudden loss in bank asset value would prevent full conversion, thereby better protecting contingent capital investors from losses.
He even addresses Julie Dickson’s proposal (although not her fabricated assertion, unchallenged by the press, that fixed-dollar conversion is universally favoured):
In other words, for the benchmark contingent capital bond, at a point just before conversion, there would need to be a sudden asset value loss exceeding 2% to prevent full conversion, while for the contingent capital bond with e = 1%, at a point just before conversion, there would need to be a sudden asset value loss only slightly more than 1% for bondholders to sustain a conversion loss. This finding has implications for recent regulatory proposals that would have contingent capital convert only when a bank was in dire straits and close to being seized by regulators. [footnote] Delaying conversion to a point when the value of original shareholders’ equity is low raises the new issue yields on contingent capital.
footnote: Canada’s superintendent of financial institutions, Julie Dickson, proposes that the conversion trigger for contingent capital would be “when the regulator is ready to seize control of the institution because problems are so deep that no private buyer would be willing to acquire shares in the bank.” Financial Times, April 9, 2010.
Update, 2010-6-6: A new reader has very kindly provided extensive commentary on my critique of this post. He claims (as paraphrased by me, JH):
(i) New equity issues from banks are not structurally equivalent to CC conversion : New equity makes extant debt safer; therefore transfers value from extant equity holders to debt holders; therefore a decline in equity price is expected. This is not the case when CC is converted.
JH – By this reasoning, my reference to the 14% new issue discount on the CIBC recapitalization is not relevant. Well …maybe!
(ii) CC holders experience a regime change on conversion and the original maturity date does not apply. The new equity may be sold or held, depending upon the holders’ views on the stock. If the stock price rises from the trigger price, the noteholders could even realize excess returns. Thus, the CC may be thought of as being default-free as of the conversion date.
JH – Well, you can bet this is the line that the salesmen will take! A lot of it depends upon perspective: it may be true from the bank’s point of view, the market’s point of view and the regulators’ point of view … but, naturally enough, I am considering it from a specialist bond managers’ point of view: who will at the very least see the risk/return profile of the portfolio visibly change; whose mandate will almost certainly prohibit the holding of equity; and who will very likely be forced to sell the stock at whatever it will fetch which (due to the ‘cascading stop-loss effect’ at the very least) will likely be lower than the conversion price.
Additionally, the reasoning incorporates the assumptions that all mathematical models must incorporate, at least to some degree: that there is infinite liquidity and that assets will be fairly priced in the future. The credit crunch has reminded us of just how battered these assumptions can be during a crisis; as a practitioner, I must take a jaundiced view.
(iii) Bank asset values jump, therefore CC is in fact credit-risky; but credit risk declines with higher trigger points
In the presence of jumps, credit risks result from the potential for the equity value to jump over the trigger point; therefore the CC will convert at a higher price than market, therefore the CC holders will experience a loss; therefore the CC is credit risky.
But importantly, CC is less credit risky than sub-debt and, by reducing leverage, will facilitate new issues of equity. It is also important to note that the credit risk introduced by the jump process declines with higher trigger/conversion prices.
JH – Again, perspective is important; a specialist bond manager (or bond portfolio manager within an integrated firm, for that matter) will not view the paper as having minimal credit risk when the trigger price is 99.9% of the current stock price. Additionally, the significant amount of duration risk at this limiting point will make such an issue very hard to integrate into a well defined portfolio.
There may well be a branch of bond mathematics that deal with this question, but I am not aware of it: I am sufficiently arrogant to claim that if I am not aware of a branch of bond mathematics, then at least 95% of bond portfolio managers are similarly ignorant.
As an unconstrained bond manager, I would be sorely tempted to buy a put on the equity, with the strike price equal to the conversion price and view the CC + put as a package. My view on the attractiveness of the package would be heavily influenced by the net yield of the continuing position. However, the chances of me, as a bond specialist, of having a mandate that allows the purchase of equity puts are infinitesimal and there will be asset allocation problems at the most integrated of management firms. I think that this area becomes hedge fund territory.
Update, 2010-6-6: My correspondent was Prof. Pennacchi. He has given me permission to quote his remarks in full, which I have done in the post Pennacchi Discusses CoCo Structural Model.
[…] PrefBlog Canadian Preferred Shares – Data and Discussion « A Structural Model of Contingent Bank Capital […]
[…] the first update to the post A Structural Model of Contingent Bank Capital, when responding to Prof. Pennacchi’s commentary (then anonymous, then later quoted in full […]
@ the author of the article: what other structural model for assessing the implication of contingent capital would you recommend, if you oppose the one by pennacchi?
[…] question in the comments to my old post A Structural Model of Contingent Bank Capital led me to look up what Prof. George […]
@msquared: I like Pennachi’s more recent proposal much better (see Contingent Capital: The Case for COERCs).
It addresses my concern about the potential for the converted bondholders to sell at the conversion price by making them mere guarantors of a deeply-discounted rights issue; this forces the inherent uncertainty onto the shoulders of the equity holders, where it belongs.